How far away is it? Is there enough distance to the coast? At what distance is the freighter? In the age of GPS and chart plotters with AIS, these questions are easy to answer. A glance at the display is enough to solve the usual navigation problems.
This is undoubtedly practical and convenient, but also boring. The omnipresence of technology means that seafaring loses some of its adventurous character and the intensity of the experience. Traditional practices are being forgotten. Even if you no longer necessarily need them in everyday life - with a few simple tricks and aids, distances and bearings can be estimated without electronics. And by the way, manual navigation is a great way to keep children and crew busy.
The geographical range of vision
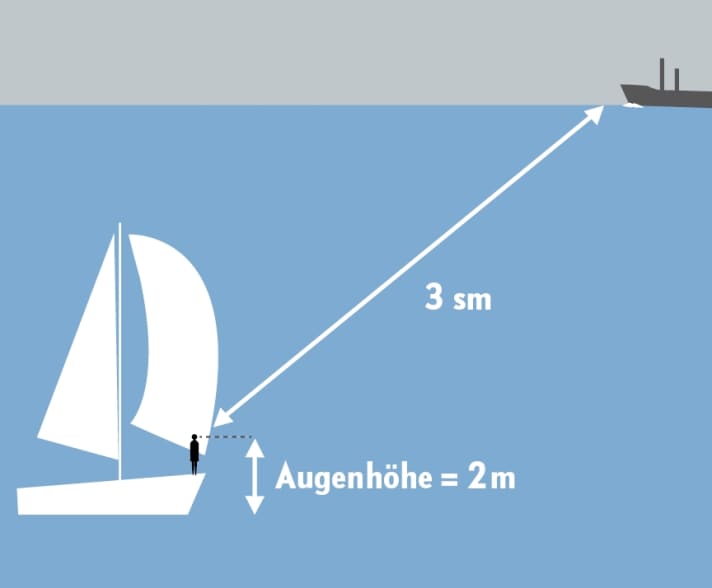
To estimate the distance of objects on the water, the first question is: How far can you see at all? Without obstacles such as mountains, rain showers, haze or fog, the curvature of the earth puts an end to the view. As the distance increases, the objects slowly but surely disappear behind the sky. How far the horizon is from the observer can be calculated using Pythagoras' theorem from the earth's radius and eye level.
Assuming that the eye level in the cockpit is around two metres, this results in a visible horizon of just under three nautical miles. This gives you a good reference point, for example to estimate the distance to other ships. For example, if you see a freighter and can recognise its full freeboard down to the bow wave, it is at most three nautical miles away. If the freeboard is cut off at the bottom, the freighter is running behind the chine and is more than three miles away.
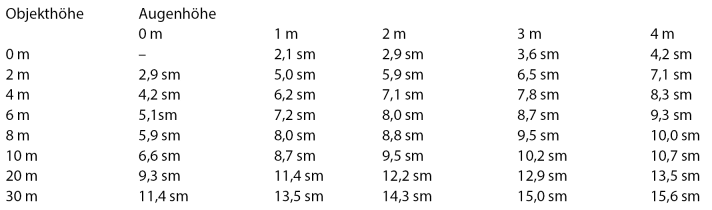
With the knowledge of the geographical visibility (see table), the distance to the coast can also be estimated. To do this, simply vary the eye level by sitting on the cockpit floor or climbing onto the superstructure. This changes the eye level from around one metre to up to four metres. If you now observe when the surf zone (object height zero metres) can be seen, you can draw the opposite conclusion about the distance.
On hot summer days, however, the system can be deceptive - due to the different air temperatures in the border area between water and land, mirages similar to a mirage are possible. The coasts are distorted in height and can be seen earlier than theoretically calculated.
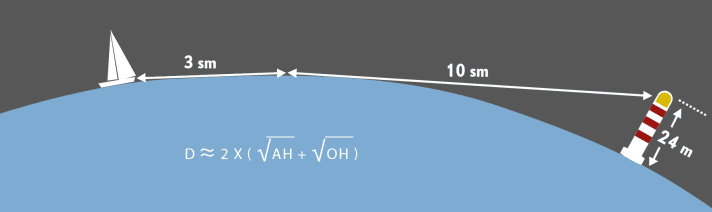
Geographical visibility is particularly useful for determining the distance to beacons with a known height (OH) at night. The fire flashes on the chine when your own horizon intersects with that of the tower.
Self-made Jacob's staff
If the height of the object is known, the distance to an object on the water or on land can also be determined using the ray theorem. This involves measuring the angle between the upper edge of the object and the horizon. This is because the ratio of the actual height of the object and the image size determined at a known distance can be set in relation to the distance from the object.
Sounds complicated, but it's not. To determine the height of the picture, you first make a rudimentary Jacob's staff as an aid. You will need a 30 centimetre long ruler and a piece of ribbon. Place the cord around the centre of the ruler and secure it with some tape. Then measure 60 centimetres on the cord and tie a knot. To measure, hold the ruler at head height in front of you with an outstretched arm so that the knot on the line reaches right up to the tip of your nose. This means that the scale of the ruler is about 62 centimetres from your eye. Now aim at the object and read off the height of the image from the ruler. The approximate distance from the object in nautical miles is calculated by dividing the actual height in metres by three times the measured height in millimetres.

If, for example, the former listening tower near Pelzerhaken, which is clearly visible around Neustädter Bucht, is targeted using this method, the following measurements may be obtained, as we did in the experiment:
A height of 26 millimetres is read off the ruler, and the nautical chart shows that the tower height is 86 metres above chart datum. The listening tower should therefore be about 1.1 nautical miles away. A look at the plotter reveals an actual distance of 1.2 nautical miles. The measuring method is therefore surprisingly accurate.
Distance measurement using a reticle in binoculars works according to the same principle. Due to the different distance to the eye and the different graduation of the reticle, the multiplier and the units in the formula also change.
However, the devil is in the detail, as it is much more difficult to read the height correctly in rough seas, both on the ruler and in binoculars. In addition, errors are caused by the curvature of the earth when objects are further away. If the landmark is behind the horizon for the observer, it appears too low as the lower part is cut off. This problem can be corrected with the so-called ridge depth, but the overall calculation becomes more complicated. Caution is also necessary when specifying heights. While the height above the map datum is given for mountain peaks, for beacons it is the height of the lantern above datum or the height of the building above the ground.
Thumb jump
The so-called thumb jump is also based on the ray theorem. One eye is squeezed shut and an object on land is aimed at with the thumb with the other arm outstretched. The eye is then changed, causing the object to jump in relation to the thumb. If you can estimate the distance of the jump on land, you also know how far away you are from the object, because the distance of the jump - multiplied by 10 - gives you the distance. The problem with this, however, is that without knowing the distance of the jump, it is not possible to judge the distance.

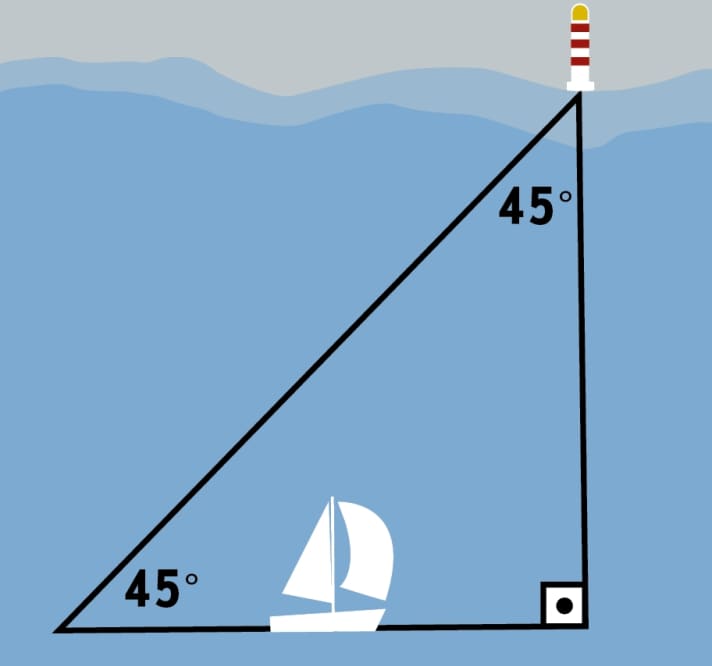
Bearing and logging
If you have a calibrated log on board, you can also use it to determine the distance to other objects, provided the ship's course passes them. The method is called a four-point bearing: if the object is located at 45 degrees to the course, the log reading is noted or the day counter is set to zero and the boat continues sailing without changing course until the object is abeam. As the two bearings and the course line form a right-angled and isosceles triangle, the distance sailed between the bearings corresponds to the distance to the object. Of course, the object must not move in the meantime.